One of the items which popped up in my FeedDemon Reader a while ago was a Blog post from a group called Sustainable Nano. They are: “The Center for Sustainable Nanotechnology is an initiative funded by the National Science Foundation to carry out research that will enable the development of sustainable, societally beneficial nanotechnologies. We are a group of well-connected but geographically diffuse scientists—at the University of Wisconsin-Madison (Hamers & Pedersen groups), University of Wisconsin-Milwaukee (Klaper group), the University of Minnesota (Haynes group), the University of Illinois at Urbana-Champaign (Murphy group), Northwestern University (Geiger group), and the Pacific Northwest National Laboratory (Orr).” It’s a neat website with plenty of interesting posts – I do like poking around in it.
Anyway to the post in question: “Space Elevator: A Lasting Dream for a Sky-reaching Tree“. The post describes the basics of the space elevator and how a product like carbon nanotubes, one of their group’s focus, could make it all possible. Pretty standard stuff, but the graphics are worth commenting on…
 The first graphic shows how a space elevator is “held up” by using the comparison to holding a stick with a rope attached to it and, the other end of the rope attached to some sort of counterweight. Spin the rope about your head (or, in the post’s example, spin your entire body) and, if you’re going fast enough, the rope will stick out straight from you towards the counterweight simulating the appearance of a space elevator. This is a common enough analogy, but does have its flaws. A space elevator is held up by balancing the forces of gravity and centrifugal force but this analogy is only demonstrating the centrifugal force portion. You (or the stick) have taken the place of gravity by holding the “earth-end” of the tether and keeping the counterweight from flying away. But I can’t think of a better way to demonstrate it and it does have the advantage of quickly being able to demonstrate the basic idea. In the graphic though, it shows Geostationary orbit (GEO) much closer to the counterweight than to the earth and the center of mass of the system at GEO (that’s where the arrows in the graphic seem to be pointing to). Using the standard Edwards/Westling model, the elevator tether is 100,000 km long while GEO is approximately 35,700 km above the surface, i.e. much closer to earth than to the counterweight at the end of the tether. Regarding the location of the center of mass of the system, it needs to be above GEO. I, myself, used to erroneously think that the center of mass would be at GEO and have visited this topic before. Dr. Blaise Gassend wrote up a simple explanation of why the center of mass has to be ABOVE geosynchronous (geostationary – GEO) orbit.
The first graphic shows how a space elevator is “held up” by using the comparison to holding a stick with a rope attached to it and, the other end of the rope attached to some sort of counterweight. Spin the rope about your head (or, in the post’s example, spin your entire body) and, if you’re going fast enough, the rope will stick out straight from you towards the counterweight simulating the appearance of a space elevator. This is a common enough analogy, but does have its flaws. A space elevator is held up by balancing the forces of gravity and centrifugal force but this analogy is only demonstrating the centrifugal force portion. You (or the stick) have taken the place of gravity by holding the “earth-end” of the tether and keeping the counterweight from flying away. But I can’t think of a better way to demonstrate it and it does have the advantage of quickly being able to demonstrate the basic idea. In the graphic though, it shows Geostationary orbit (GEO) much closer to the counterweight than to the earth and the center of mass of the system at GEO (that’s where the arrows in the graphic seem to be pointing to). Using the standard Edwards/Westling model, the elevator tether is 100,000 km long while GEO is approximately 35,700 km above the surface, i.e. much closer to earth than to the counterweight at the end of the tether. Regarding the location of the center of mass of the system, it needs to be above GEO. I, myself, used to erroneously think that the center of mass would be at GEO and have visited this topic before. Dr. Blaise Gassend wrote up a simple explanation of why the center of mass has to be ABOVE geosynchronous (geostationary – GEO) orbit.
The second graphic, the one referring to the almost-certainly necessary taper of the elevator tether is one that I’ve seen in similar format several times before. I’ve wanted to address it before, but just haven’t – I’ve been too lazy to try and draw my own version of the “correct” ratios for a tethered taper (I’m just familiar enough with Photoshop to be dangerous…). You’ll note that the blog post shows the tether increasing from a point at the earths surface to something much wider at GEO and then reducing back to a point at the counterweight. Ignoring the location of GEO (the same as in the first graphic), the idea of the tether widening from the earth to GEO and then narrowing from GEO to the counterweight is correct. But the ratio is wrong:
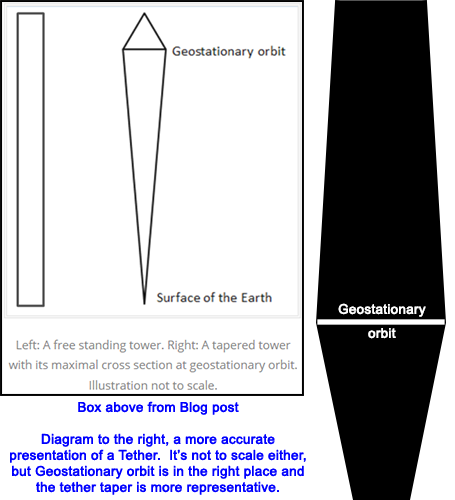
Creating my own model took me a lot longer than I had first thought – I redid it a half-dozen times before I had something I thought was worthwhile. Of course it’s not to scale either, but the ratio of the taper width at the earth’s surface (13.52) to its width at GEO (35.44) to its width at the counterweight (23.88) is correct. Also, given the shown length of the tether, the location of GEO is correct. The graphic is greatly “squooshed” of course, being much shorter than a real tether in this scale (by several orders of magnitude). But the difference between the length and the width of the tether demands this type of alteration.
One other thought; I think when most people look at drawings of tether taper, they assume that it’s the width of the tether which must alter. That’s not necessarily the case. It can also be the thickness and that, I think, would have advantages. If the width of the tether was constant (once you’re above the atmosphere – in the atmosphere it may well be a cable), then you don’t have to design a climber which can accommodate varying widths; much easier, I think to design a climber for a tether with a varying thickness. But then again, maybe it will be something like a Hoytether.
Anyway, enough. Where did I get my numbers? They came from the most excellent spreadsheet developed by long time friend of the space elevator Maurice Franklin and which you can find by clicking on its page link at the top of blog (The SE Analysis Spreadsheet). I’ve blogged about this before, and I’d like to encourage readers to play around with it – when you do, you really begin to get a feel for the physical constraints that engineers and scientists have to deal with in the real world. I used his Edwards/Westling Baseline model with no changes.

I think that the basic rule that absolutely has to be met is simpler:
The total upward force generated by centrifugal acceleration acting on the mass of the SE must exceed the total downward force generated by gravity acting on that same mass.
The words “upward” and “downward” aren’t really necessary in that sentence, but do make it a bit clearer; the same is true of the two instances of “total.” The force exerted on the anchor by the SE will be the difference between those two forces.
I don’t think that my rule implies Ted’s rule “the center of mass has to be above GEO” because I don’t think that it does have to be above GEO. (continued on next rock…)
“The Center of Mass”
I hate the use of that term in these discussions, because I don’t think it is applicable or well defined. For a long thin object like the SE, the center of mass would be the point along its length at which half the total mass is on one side and half on the other. That’s pretty meaningless for the SE, where the basic physics are determined by two forces that vary drastically along its length — gravity and centrifugal — and the location of mass in those fields.
Moreover, “center of mass” is used in physics as a simplification: the use of a point mass instead of the distributed mass of a real object. It’s the equivalent of “Assume the cows are all spheres…” We can’t assume that the SE is a point mass.
Here’s a gedankenexperiment: assume we have an extremely, perhaps infinitely, strong material to build the SE with and that it’s very light, say 1 g per km. Now imagine an SE anchored at the Earth end like always and with a 100 ton spacelab attached 1 km below GEO. From the top of the spacelab our wonder cable extends out as far as is necessary to a 1 ton counterweight. I haven’t done the arithmetic, but intuitively it’s likely that the counterweight is only a few hundreds of thousands of kilometers out. Where’s the center of mass? In the middle of the spacelab, below GEO.
Look at it another way. Assume for your gedankenexperiment, your spacelab is only 1 km above the earth and attached to a tether, it will obviously fall to earth as it’s not travelling fast enough. Increase the tether length to 1,000 km and the spacelab will still fall – again, it’s not travelling fast enough. You can continue to increase the altitude (and thus the speed of the spacelab), but it will still fall until you reach GEO. You have to get to GEO in order to be travelling fast enough to stay above a fixed point on the earth. The center of mass of the system has to be at GEO (or above it) to keep the system stable; not falling back to earth.
@Ted:
Not true. You have to have sufficient mass far enough above GEO to keep the system stable. In my example I had a large mass just below GEO where Earth’s gravity is down to 0.23 m/s² or 0.024 g and a much smaller mass WAY above GEO, where acceleration due to centrifugal force is, say 29.4 m/s² or 3.0 g. The 1 ton counterweight (weight 3 tons) is more than sufficient to hold up the 100 ton spacelab (weight 2.4 tons), even ignoring the effect of centrifugal force on the spacelab.
Can we agree on this? Everything in the Space Elevator system that is located below GEO; tether, climbers and your gedanken space station, exerts a net downward force on the system. And everything in the Space Elevator system that is located above GEO, tether, climbers and the counterweight (apex anchor), exerts a net upwards force on the system. This is true BY DEFINITION, yes?
Yes, though I’m not sure what “by definition” is saying in that sentence. It’s true because of physics, not because of some definition. Also I’d quibble about the idea that the various masses are exerting force. It’s gravity and centrifugal acceleration acting on the masses that exerts force.
I just dug up a Hyperphysics page that I modified years ago. The bottom topic allows you to specify a position on an SE in kilometers above the anchor. It calculates the velocity relative to the center of the Earth, acceleration due to centripetal force, acceleration due to Earth’s gravity, and the effective gravity (sum of the prior two).
Centripetal Acceleration on Elevator It’s a tad easier to use than the spreadsheet.